How to Find Z Score in Excel – Step by Step Guide

Introducing Z-Score Mastery in Excel

Grasping the Basics of Z-Score

Mastering the use of Z-scores in Excel starts with understanding the fundamentals. I regard Z-scores as a statistical measurement that reveals how a particular data point compares to the average of a dataset. It’s like finding out whether your test score is above or below the average without knowing your classmates’ marks – this is what Z-scores help with.

They pinpoint whether a value is common or rare in a given set by measuring its distance, in standard deviations, from the mean.

Why Excel is Your Go-To for Z-Score Analysis

Excel shines as a tool for Z-score analysis because of its simplicity and accessibility. With its vast array of functions and formulas, Excel allows me to effortlessly conduct statistical analyses without requiring the advanced know-how of specialized statistical software. It’s quite remarkable – with just a few keystrokes, I can transform raw data into meaningful Z-scores, enabling me to identify outliers and comprehend data distributions.

From marketers optimizing campaigns to educators grading tests, Excel’s user-friendly interface supports a multitude of professionals in their analytical endeavors. Moreover, its built-in functions streamline the entire process, making Excel an indispensable part of my statistical toolbox.

Excel is the trusted companion I turn to time and again for Z-score analysis, regardless of the complexity of the dataset at hand.

Why Use Z Scores?

Z scores are used to:

• Identify outliers (extremely high or low values)
• Compare scores from different datasets
• Transform data for further analysis

 

The Mathematical Underpinnings of a Z-Score

Breaking Down the Z-Score Formula

When we talk about breaking down the Z-score formula, we’re delving into the elegant simplicity of how Z-scores are calculated. The formula, Z = (X – Mean of the dataset) / Standard Deviation of the dataset, serves as a ruler to measure how many standard deviations a data point, X, is from the mean. It’s like uncovering a hidden story within the numbers, revealing how far away an individual score is from the crowd.

This principle holds true regardless of the scale or units of the original data, thus allowing for cross-dataset comparisons and contributing to a consistent analytical framework.

Understanding AVERAGE, STDEV.S, and STDEV.P functions

The AVERAGE, STDEV.S, and STDEV.P functions are the foundational blocks in Excel for statistical analysis, and understanding each one is critical for accurate Z-score calculations. The AVERAGE function, as its name suggests, provides the arithmetic mean of a set of numbers – it’s what we use to find the center or the ‘average’ experience in a dataset.

= AVERAGE(number1, [number2], …)

• Number1 Required. The first number, cell reference, or range for which you want the average.
• Number2, … Optional. Additional numbers, cell references or ranges for which you want the average, up to a maximum of 255.

When I look at STDEV.S and STDEV.P, they represent two different methods for calculating standard deviation, which is a measure of the amount of variation or dispersion of a set of values. STDEV.S calculates the standard deviation for a sample of a population. Conversely, STDEV.P is used when I want to assess the standard deviation for an entire population.

=STDEV.P(number1,[number2],…)

• Number1    Required. The first number argument corresponding to a population.
• Number2, …    Optional. Number arguments 2 to 254 corresponding to a population. You can also use a single array or a reference to an array instead of arguments separated by commas.

It’s fascinating to note that the difference between these two lies in the ‘denominator’ used in their formulas. STDEV.S uses ‘n-1’ (where ‘n’ is the number of observations), a method known as Bessel’s correction, which corrects the bias in the estimation of the population variance and standard deviation. On the other hand, STDEV.P divides by ‘n’, assuming a full overview of the population is available.

When it comes to which one to use for Z-score calculations in Excel, it’s essential to choose the correct function to reflect the nature of the data, whether it’s from a sample or the entire population.

By integrating these functions correctly, I ensure the Z-scores derived are both accurate and meaningful in the context of the analysis being undertaken.

 

How to Find Z Score in Excel

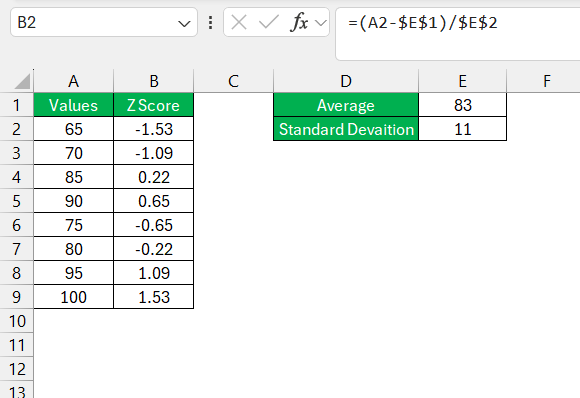
STEP 1: Enter the data in Column A from A2 to A9.

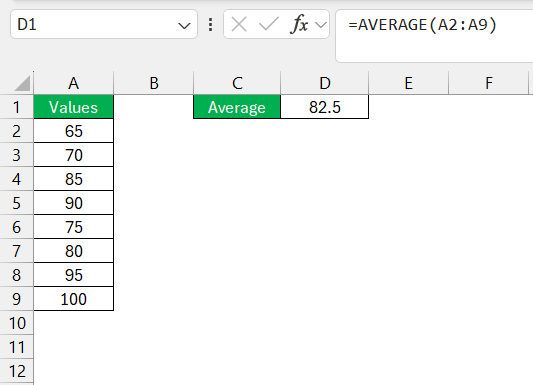
STEP 2: To calculate the mean of the dataset, use the AVERAGE function in Excel.

=AVERAGE(A2:A9)

In this example, the mean is 82.5.

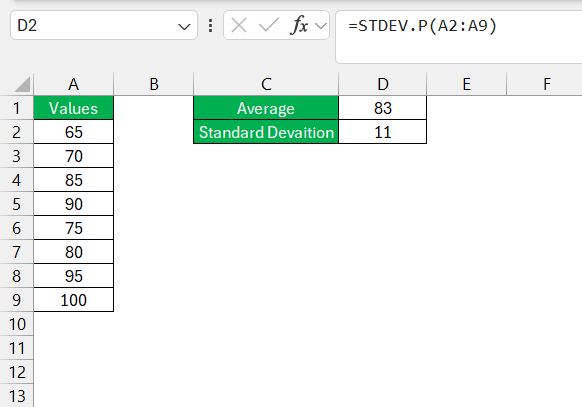
STEP 3: Next, calculate the standard deviation using the STDEV.P function (for population) or STDEV.S (for sample data). In this example, we’ll assume the dataset represents a population.

=STDEV.P(A2:A9)

The result is 11.

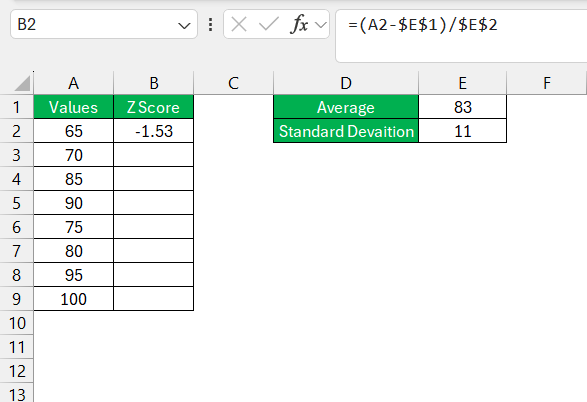
STEP 4: Now that we have the mean and standard deviation, we can calculate the Z score for each data point using the formula:

=(A2 – $E$1) / $E$2

• $E$1 is the absolute reference to the cell where the mean is stored.
• $E$2 is the absolute reference to the cell where the standard deviation is stored.

STEP 5: Drag the formula down from B2 to B9 to calculate the Z scores for all the data points.

 

Interpreting Your Z-Score Results

What Your Z-Score Tells You

You now have Z scores for each data point in Column B. A Z score tells you how far away a value is from the mean:

• A Z score of 0 means the data point is exactly at the mean.
• A positive Z score indicates the data point is above the mean.
• A negative Z score indicates the data point is below the mean.

For instance, if the Z score of a data point is -1.53, that means it is 1.53 standard deviations below the mean.

A Z-score provides me with a standardized notion of where a data point sits in relation to the mean of the dataset. A score close to 0 indicates the value is near the average, while a positive or negative score highlights how many standard deviations away from the mean the value is situated. A positive Z-score tells me a data point is above average, whereas a negative one signifies it’s below average.

Understanding Z-scores gives me the power to quantify the unusualness of a data point. For instance, a Z-score of 2 means the value is two standard deviations more than the average, which could represent an exceptional case in the context of a given dataset.

A clear understanding of Z-scores allows me to make informed decisions in data analysis, research, and operational strategies. It’s a fundamental tool in my statistical arsenal.

 

FAQ: Your Z-Score Queries Answered

How to calculate z test in Excel?

To calculate a z-test in Excel, use the formula =(sample_mean-population_mean)/(population_standard_deviation/SQRT(sample_size)) to compute the z-score. Then utilize =NORM.S.DIST(z_score, TRUE) to find the p-value. Compare this p-value to the significance level to decide if the null hypothesis should be rejected.

How Do I Convert Z-Scores to Percentiles in Excel?

In Excel, convert Z-scores to percentiles using =NORM.S.DIST(z_score, TRUE). This formula gives you the percentile rank, telling you the percentage of scores below the z-score in a standard normal distribution.

Can Excel Automatically Refresh Live Data for Real-Time Z-Score Analysis?

Yes, Excel can automatically refresh live data for real-time Z-score analysis when using external data connections. Set up your data source to refresh at regular intervals by going to Data > Queries & Connections > Properties and adjusting the refresh settings as needed.

How Can I Ensure My Z-Score Calculations Are Error-Free?

To ensure error-free Z-score calculations, double-check your data for accuracy and completeness. Use Excel functions like =AVERAGE() for the mean and =STDEV.S() for the standard deviation correctly. Verify that each part of the Z-score formula is referencing the correct cells or ranges.

What does z scored use for in our everyday life?

In everyday life, Z-scores are used to benchmark individual performance or measurements against a norm. It’s applied in academics to compare test scores, in health to interpret medical results against standard values, and in personal finance to assess spending habits relative to an average.