How to Calculate Average Degrees on a Compass in Excel

When working with directional data such as wind directions, navigation logs, or sensor readings, calculating the average of compass angles is not as straightforward as using the AVERAGE function. This is because compass values wrap around at 360 degrees. For example, the average of 350° and 10° should be 0° instead of 180°. In this article, we will explore how to correctly calculate the average degrees on a compass using Excel formulas, trigonometry, and VBA.

Key Takeaways

• Regular arithmetic averages do not work for compass angles due to the circular scale.
• Convert degrees into radians and then calculate sine and cosine components.
• Take the average of sine and cosine values before converting back to degrees.
• Excel functions like RADIANS, SIN, COS, and ATAN2 are essential for this calculation.
• VBA can automate the calculation for large datasets or repeated tasks.

Why Regular Averages Fail for Compass Angles

If you try to average 350° and 10° using =AVERAGE(350,10), Excel will return 180°, which is not correct. On a compass, both values are close to North, so the average should be 0°. This happens because angles are circular, and simple arithmetic does not account for wraparound at 360°.

Understanding Compass Degrees

When it comes to understanding compass degrees, you’ll want to start with the basics: how they map out directions. A compass is essentially a circle divided into 360 degrees, with North corresponding to both 0° and 360°. East is at 90°, South at 180°, and West at 270°. Knowing these main points is crucial as they serve as the foundational markers for any directional calculations

To average degrees accurately, particularly when your headings span across the 0°/360° line, it’s important to use a method that considers the circular nature of the compass. For instance, if your headings are 355° and 5°, a simple arithmetic mean would yield 180°, which is incorrect. Instead, use the circular mean, which in this case computes to 0°.

A handy tip is to convert degrees to radians when performing calculations, then convert them back to degrees. This method minimizes errors often encountered with degree arithmetic. With a proper understanding of how compass degrees function, you’ll be well-equipped to handle both simple and complex direction calculations with ease.

Traditional vs. Modern Compass Reading

Traditional compass reading relies heavily on the physical compass, where you interpret the needle’s position relative to marked degrees. This method requires a solid grasp of magnetic north and adjustments for declination, which is the difference between true north and magnetic north [Insert image of a traditional compass with annotations]. The traditional method is durable, low-tech, and does not rely on batteries, making it exceptionally reliable in off-grid situations.

Modern compass reading, on the other hand, leverages digital technology, via apps and GPS devices that provide not only direction but also real-time data on location, speed, and elevation. Digital compasses often automatically adjust for declination, offering greater precision without requiring calculations from the user. They are user-friendly and often integrate seamlessly with mapping software for comprehensive navigation solutions.

In comparing the two, traditional compasses are unmatched in simplicity and durability, while modern digital options offer unparalleled accuracy and additional data. They can sometimes be limited by battery life or technical malfunctions, though. For those who value precision and additional navigational data, modern digital compasses are best. Traditional compasses, ideal for minimalist adventurers, offer reliability without reliance on technology.

How to Calculate Average Degrees on a Compass in Excel

Converting Degrees to Radians

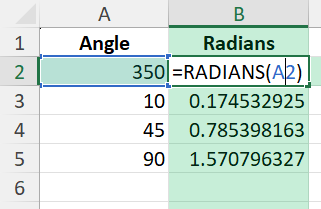
The first step is to convert compass degrees to radians since Excel’s trigonometric functions use radians:

=RADIANS(A2)

Repeat this for all angle values in your dataset.

Calculating Sine and Cosine Components

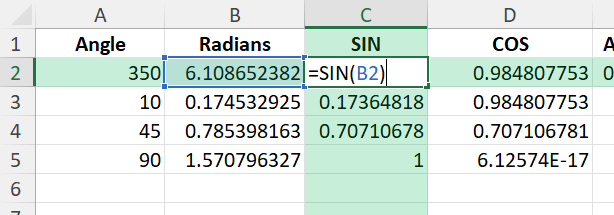
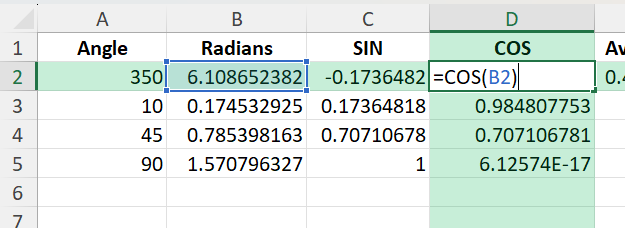
For each angle in radians, calculate sine and cosine:

=SIN(B2)
=COS(B2)

These values represent the directional components of each angle.

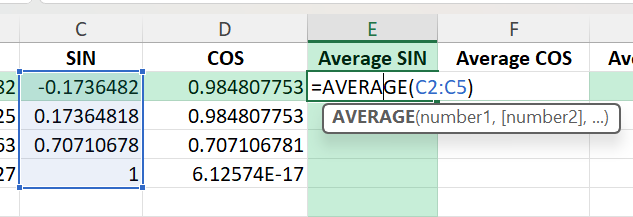
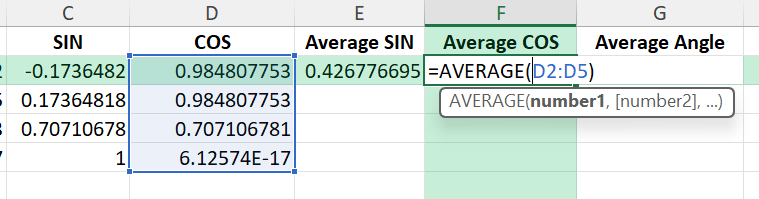
Averaging Sine and Cosine Values

Once you have all sine and cosine values, calculate their averages:

=AVERAGE(C2:C5)   ' Average SIN
=AVERAGE(D2:D5)   ' Average COS
 

Calculating the Final Average Angle

Now use ATAN2 to find the angle from the average sine and cosine values:

=DEGREES(ATAN2(AverageSIN, AverageCOS))

This formula gives you the correct mean angle in degrees.

Common Mistakes and Tips

Using AVERAGE directly: This fails for circular data. Always use trigonometric methods.

Forgetting radians: Ensure you convert degrees to radians before applying SIN or COS.

Negative angles: ATAN2 may return negative results. If needed, add 360 to keep values in the 0–360 range.

Data validation: Make sure angle inputs are numeric and within 0–360.

Bonus Tips and Advanced Scenarios

Weighted Averages: You can extend the formula by applying weights to certain angles if needed.

Power Query: Preprocess directional data using Power Query and then apply trigonometric methods in Excel.

Dynamic Named Ranges: Use dynamic ranges with tables so your average angle updates automatically when new data is added.

VBA Option for Automating the Process

You can also use a VBA function for convenience:

Function AverageCompassAngle(rng As Range) As Double
    Dim cell As Range
    Dim sumSin As Double
    Dim sumCos As Double
    Dim count As Long
    
    For Each cell In rng
        If IsNumeric(cell.Value) Then
            sumSin = sumSin + Sin(Application.Radians(cell.Value))
            sumCos = sumCos + Cos(Application.Radians(cell.Value))
            count = count + 1
        End If
    Next cell
    
    If count > 0 Then
        AverageCompassAngle = Application.Degrees(Atn2(sumSin / count, sumCos / count))
    Else
        AverageCompassAngle = CVErr(xlErrDiv0)
    End If
End Function

After adding this function in the VBA editor, you can use =AverageCompassAngle(A2:A5) directly in your sheet.

Use Cases for Average Compass Angles

Weather Data: Calculate average wind direction from multiple readings.

Navigation: Find the mean heading of a vessel or aircraft.

Surveying: Determine the average bearing in field measurements.

Sports Analytics: Analyze average kick or throw directions in performance studies.

Manufacturing: Track machine tool orientation averages.

FAQ

Why can’t I just use the AVERAGE function for compass angles?

Because compass values wrap around, a direct arithmetic average may produce results far from the true mean.

What if my result is negative?

You can add 360 if the ATAN2 output is negative. For example: =MOD(Result,360).

Can I use this method for weighted averages?

Yes, by multiplying sine and cosine values by their weights before averaging.

Is this method available in all Excel versions?

Yes, since it uses basic functions (SIN, COS, ATAN2, RADIANS, DEGREES) available in all versions.

Can VBA make this easier?

Yes, VBA allows you to call =AverageCompassAngle() directly, saving time on manual formulas.