How to Use Fibonacci Sequence Formula in Excel

If you’re anything like me, you’ve probably heard about the Fibonacci Sequence in school or while scrolling through random trivia posts online. But here’s the fun part — I recently figured out how easy (and actually useful) it is to generate the Fibonacci Sequence directly in Excel.

Let me walk you through exactly how to create the Fibonacci Sequence Formula in Excel.

Key Takeaways:

• Fibonacci Sequence is a series where each number is the sum of the previous two numbers, starting from 0 and 1.
• Fibonacci numbers appear everywhere — in nature, architecture, trading charts, and even art designs.
• Excel makes it super easy to create a Fibonacci Sequence formula using simple addition or advanced methods like Binet’s Formula.
• Using ROW() and IF formulas in Excel helps automate and create dynamic Fibonacci Sequences without worrying about manual errors.
• Common mistakes in Excel Fibonacci calculations include wrong starting numbers, formula errors, and cell formatting issues — but they’re easy to fix with basic checks.

 

The Fascination with Fibonacci

What is the Fibonacci Sequence?

The Fibonacci Sequence is a series of numbers where each number is the sum of the two preceding numbers. It looks like this:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34 … and so on.

For example:

• 0 + 1 = 1
• 1 + 1 = 2
• 1 + 2 = 3
• 2 + 3 = 5
• 3 + 5 = 8
• 5 + 8 = 13
• …and so on.

The beauty of this sequence lies in its simplicity — just keep adding the last two numbers to get the next one. This pattern shows up everywhere — nature, art, trading charts, and even in architecture.

Historical Insights into Fibonacci

Leonardo of Pisa, known as Fibonacci, was a remarkable mathematician from the Middle Ages. Born around 1170, Fibonacci introduced the sequence that bears his name to the Western world through his book “Liber Abaci” in 1202. Though he didn’t invent the sequence—it was already known in Indian mathematics—Fibonacci’s work helped to popularize Arabic numerals in Europe, vastly improving calculations compared to the Roman numeral system.

His sequence was initially part of a problem about rabbit breeding, yet it quickly became much more than a hypothetical exercise, providing insights into natural phenomena and mathematical theory.

The Golden Ratio Connection

The Fibonacci Sequence is intimately connected to the Golden Ratio, an irrational number approximately equal to 1.6180339887. As you progress along the sequence, the ratio of two consecutive Fibonacci numbers increasingly approximates the Golden Ratio. This connection doesn’t just have mathematical significance; it’s also found in the spirals of shells, galaxies, and the proportions of artistic masterpieces.

The Golden Ratio is often regarded as a blueprint for beauty and harmony, which further elevates the allure of Fibonacci’s sequence within natural and human-made structures. The balance and symmetry observed using the Golden Ratio can be harnessed in design and architecture, showcasing the mathematical wonder born from Fibonacci’s simple numerical sequence.

 

Generating the Fibonacci Sequence Formula

Leveraging Addition for Sequence Creation

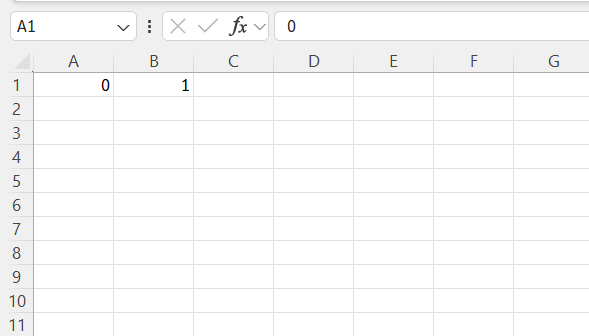
Creating the Fibonacci Sequence Formula in Excel using simple addition is both straightforward and intuitive. To start, enter the first two numbers of the sequence—0 and 1—in two adjacent cells, for example, A1 and A2.

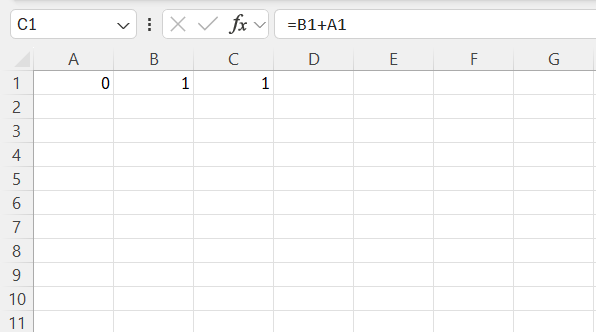
Next, in cell A3, enter the formula =A1+A2.

This formula ensures that each subsequent number in the sequence is the sum of the two preceding numbers. You can then drag the formula down through subsequent cells to extend the sequence as far as you need.

This elementary method effectively demonstrates the inherent simplicity and beauty of the Fibonacci Sequence, making it accessible even to beginners working within Excel.

Implementing Binet’s Formula

Binet’s Formula provides a direct way to calculate any Fibonacci number without iteration. It’s defined as Fn = ((φ^n – (1-φ)^n) / √5), where φ (phi) is the Golden Ratio (approximately 1.61803). Implementing Binet’s formula in Excel involves using this equation to compute Fibonacci numbers directly. To do this, use Excel’s power and square root functions.

In a cell, input =ROUND((((1+SQRT(5))/2)^A4 - ((1-SQRT(5))/2)^A4)/SQRT(5), 0), adjusting A4 to reference the cell with the desired sequence position.

This approach is advantageous for accessing large Fibonacci numbers quickly and accurately, transcending the limitations of iterative addition. While powerful, this method might produce small inaccuracies due to floating-point arithmetic when handling very large indices, but it’s a shining example of Excel’s capacity to bridge algebra and arithmetic fluidly.

Bonus Tip: Making It Dynamic with Excel’s IF Formula

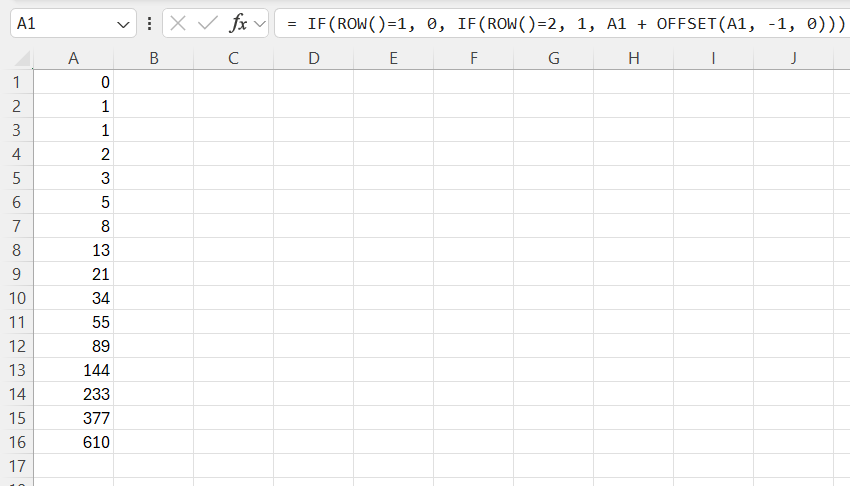
Sometimes, I like making things cleaner, especially if I’m setting up templates for others. Here’s a formula I use in cell A1 to A20 that works even if someone accidentally deletes the starting numbers:

= IF(ROW()=1, 0, IF(ROW()=2, 1, A1 + OFFSET(A1, -1, 0)))

This uses ROW() to set the first two values and calculates the rest dynamically.

 

Common Pitfalls and Solutions

When generating the Fibonacci Sequence in Excel, common pitfalls can hinder progress, but they are easily rectifiable. One frequent mistake is beginning the sequence without initializing the correct starting values, leading to incorrect calculations. Always begin with 0 and 1 to ensure accuracy.

Another issue is formula errors, particularly when using Binet’s Formula, where parenthesis placement is crucial. Ensuring their proper alignment prevents computational mistakes. When dealing with large numbers, Excel’s default cell format might not handle them well due to limitations in floating-point precision. Adjust the format to scientific notation or smaller increments to mitigate this.

In formulas involving range references, adjusting for relative and absolute references using dollar signs ($) can prevent errors when dragging formulas across cells. These solutions enhance the reliability of calculations and maintain the sequence’s integrity. As a tip, double-check each formula for accuracy and ensure that functions are correctly referenced, removing any discrepancies that could distort results.

 

FAQs

What is Fibonacci sequence?

The Fibonacci Sequence is a series of numbers where each number is the sum of the two preceding ones, starting from 0 and 1. Typically, the sequence goes 0, 1, 1, 2, 3, 5, 8, and so on. It appears in various natural phenomena, art, and architecture, celebrated for its intriguing mathematical properties and connection to the Golden Ratio.

Why is Fibonacci sequence important?

The Fibonacci Sequence is important because it appears in diverse fields, from natural phenomena to financial markets. Its relationship with the Golden Ratio offers insights into patterns found in nature and design, and its mathematical properties are fundamental in algorithm development, particularly in computer science and recursive algorithms.

What is the formula for the Fibonacci sequence?

The formula for the Fibonacci Sequence is Fn = Fn-1 + Fn-2, where the sequence starts with F0 = 0 and F1 = 1. Each subsequent number is the sum of the two preceding ones, allowing the sequence to grow indefinitely. Binet’s Formula provides a direct calculation method, using the Golden Ratio: Fn = ((φ^n – (1-φ)^n) / √5).

What is the simplest method to create a Fibonacci sequence in Excel?

The simplest method to create a Fibonacci Sequence in Excel is using basic addition formulas. Start by entering 0 in cell A1 and 1 in cell A2. In cell A3, input the formula =A1+A2. Extend this formula down the column, and it will automatically compute the sequence by summing the two preceding numbers in each row.

How does Binet’s formula work within Excel?

Binet’s Formula calculates Fibonacci numbers directly using the Golden Ratio. In Excel, input the formula =ROUND((((1+SQRT(5))/2)^n - ((1-SQRT(5))/2)^n)/SQRT(5), 0) in a cell, substituting n with the desired Fibonacci term’s position. This formula efficiently computes Fibonacci numbers without iteration, although small inaccuracies may occur with very large indices.