How to Find Horizontal Asymptotes in Excel

In this informative guide, I aim to walk you through the process of finding horizontal asymptotes using Excel. My goal is to make this complex mathematical concept accessible and straightforward, leveraging Excel’s powerful data analysis capabilities. By the end of this post, you should have a clear understanding of how to set up your data and analyze it with precision.

Key Takeaways:

• Horizontal asymptotes show the long-term behavior of a function as x approaches ±∞.
• Excel can be used to plot and visualize these asymptotes easily using formulas and graphs.
• The degree of the numerator and denominator in a rational function determines if and where a horizontal asymptote exists.
• Case-based rules help identify the asymptote value: equal degrees → ratio of coefficients, higher denominator degree → y = 0, higher numerator degree → no horizontal asymptote.
• Practical fields like economics and biology use horizontal asymptotes to model trends, limits, and saturation points in real-world data.

 

Understanding Horizontal Asymptotes

What is a Horizontal Asymptote?

In simple terms, a horizontal asymptote represents the value that a function approaches as the input (usually x) becomes very large or very small. It doesn’t mean the function ever reaches this value—just that it gets closer and closer to it.

For example, consider the function:

f(x) = 1 / x

As x becomes very large (say, 1000), the value of f(x) gets closer to 0. That’s our horizontal asymptote: y = 0.

The Concept of Asymptotes in Graphing

Asymptotes are lines that a graph approaches but never actually touches. In graphing, understanding asymptotes is crucial because they reveal long-term behavior trends of functions, particularly as they extend towards infinity. In the realm of horizontal asymptotes, these are the lines that the graph of a function approaches as the input values reach positive or negative infinity. Typically, they occur in rational functions where the degrees of the numerator and the denominator determine the presence and position of the asymptote.

Recognizing these trends allows us to make informed predictions about the behavior of complex functions.

Importance of Mathematical Analysis

Understanding horizontal asymptotes is essential in mathematical analysis as they provide insights into the behavior of functions over large domains. These asymptotes help us identify limits and continuity, offering a simplistic view of how functions behave at extremes. By understanding where these lines exist, we can predict outcomes and model real-world phenomena more accurately.

This knowledge is particularly valuable in fields like economics, engineering, and natural sciences, where trends and patterns dictate strategic decisions and actions. Horizontal asymptotes allow us to focus on meaningful data trends without getting lost in minor fluctuations.

 

How to Determine a Horizontal Asymptote

In simple terms, a horizontal asymptote represents the value that a function approaches as the input (usually x) becomes very large or very small. It doesn’t mean the function ever reaches this value—just that it gets closer and closer to it.

When you’re dealing with rational functions—that is, a function of the form:

f(x)=P(x)/Q(x)

where both P(x) (numerator) and Q(x) (denominator) are polynomials—the horizontal asymptote depends on the degree (i.e., the highest power of x) of each polynomial.

Here’s the basic rule I always follow to determine the Horizontal Asymptotes:

Case 1: Degrees Are Equal

If the degree of the numerator is the same as the degree of the denominator, then the horizontal asymptote is the ratio of their leading coefficients.

Example: f(x)=(2x+3)/(x+1) f(x)

• ​Degree of numerator: 1 (because of 2x)
• Degree of denominator: 1 (because of x)
• Leading coefficients: 2 (numerator), 1 (denominator)

Horizontal asymptote: y = 2/1 = 2

Case 2: Denominator Degree Is Higher

If the degree of the denominator is greater than the degree of the numerator, then the horizontal asymptote is y = 0.

Example: f(x) = (x+1)/(x^2+5)

• Degree of numerator: 1
• Degree of denominator: 2

Horizontal asymptote: y = 0

Because the denominator grows much faster than the numerator as x → ±∞, so the whole fraction gets closer to zero.

Case 3: Numerator Degree Is Higher

If the degree of the numerator is greater than the degree of the denominator, then there is no horizontal asymptote. But there might be an oblique (slant) asymptote, especially if the numerator’s degree is just one more than the denominator’s.

Example: f(x) = (x^2+1)/(x+1)

• ​Degree of numerator: 2
• Degree of denominator: 1

No horizontal asymptote.

 

Step-by-Step Guide to Calculate Horizontal Asymptotes

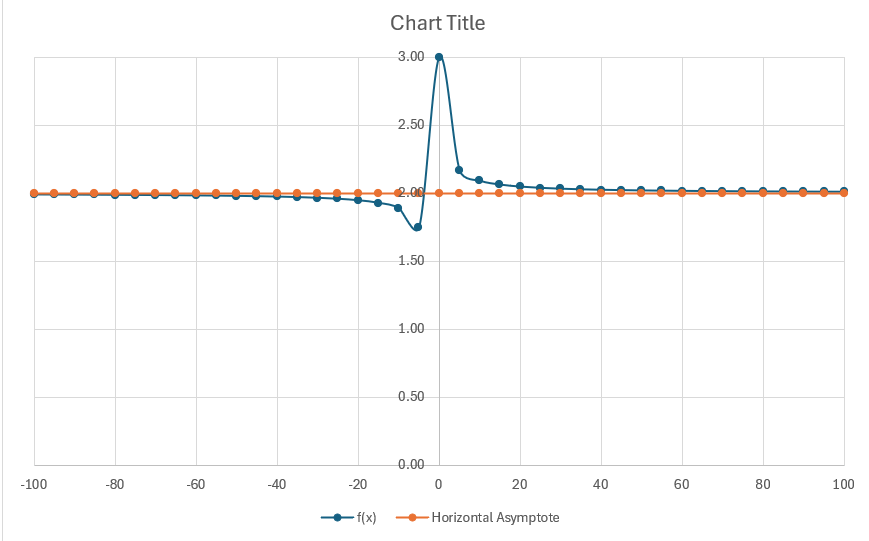
Here’s how I calculate and visualize a horizontal asymptote using Excel:

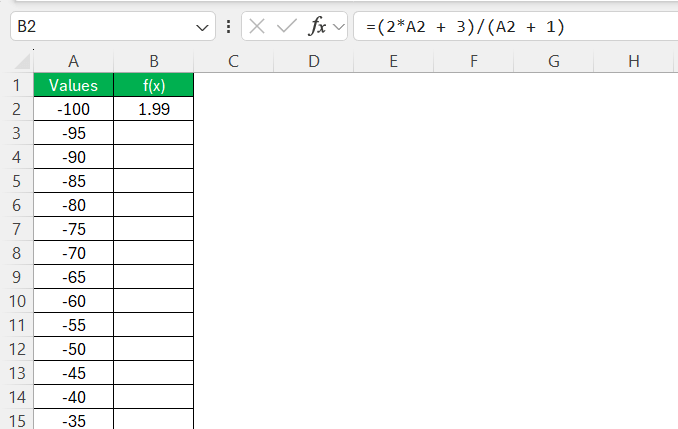
STEP 1: In Column A, list a range from -100 to 100 (or whatever range suits your function).

STEP 2: In Column B, apply the function using Excel syntax.

f(x) = (2x+3)/(x+1)

​Formula in B2 (if A2 contains x):

=(2*A2 + 3)/(A2 + 1)

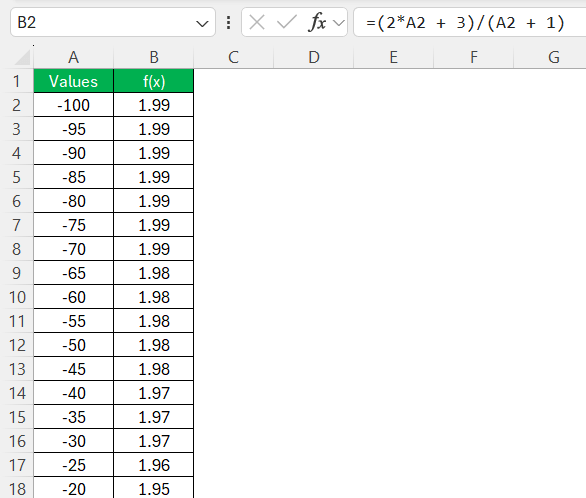
STEP 3: Drag the formula down in column B.

STEP 4: For the above function, the horizontal asymptote is:

y=2

Since the degree of the numerator is the same as the degree of the denominator, the horizontal asymptote is the ratio of their leading coefficients.

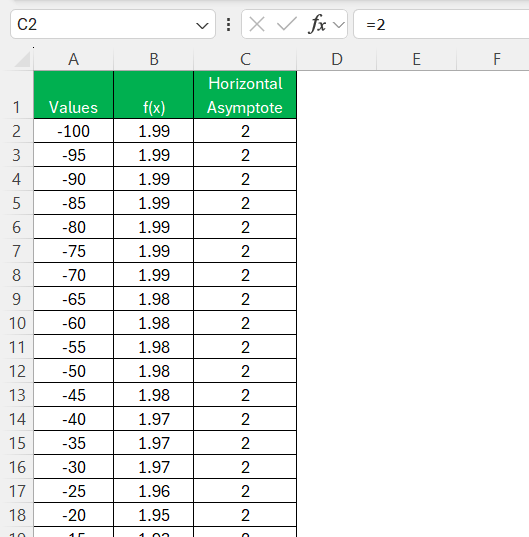
STEP 5: Add a Column for Asymptote Line

In Column C, enter =2 and drag it down to match the x-values.

 

Create Graphs with Horizontal Asymptotes in Excel

Now it’s time to see it all in action:

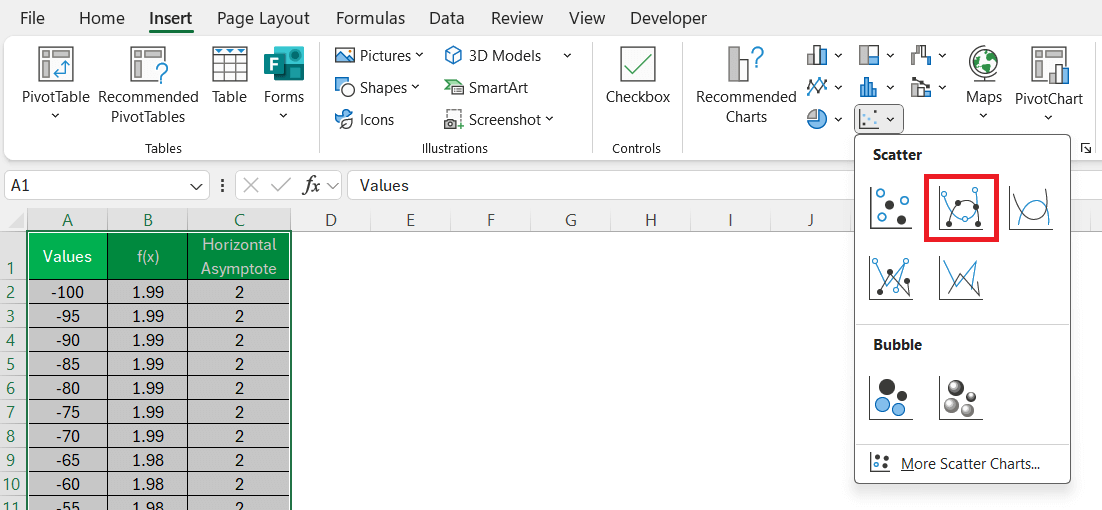
STEP 1: Select all three columns (A: x-values, B: function, C: asymptote).

STEP 2: Go to Insert → Scatter Plot with Smooth Lines.

Excel will plot the curve and the flat asymptote line—super clear and visually intuitive!

You’ll notice the function curves approach the horizontal line as x gets large or small, but never quite touch it. That’s the asymptote magic at work.

 

Practical Examples and Applications

Real-World Scenarios in Data Analysis

Horizontal asymptotes play a crucial role in real-world data analysis across various fields. For instance, in economics, asymptotes can indicate market saturation points—where increasing input no longer results in substantial output growth. This helps in modeling long-term strategic plans and forecasts.

In environmental science, asymptotes might represent the carrying capacity of an ecosystem, pointing to a population size that an environment can sustain over time. Recognizing these thresholds allows for sustainable management of resources.

In pharmacokinetics, horizontal asymptotes can illustrate the maximum concentration of a drug in a bloodstream over time, guiding safe and effective dosage recommendations.

Such scenarios demonstrate how horizontal asymptotes provide valuable insights into the essential limits and constraints of various practical phenomena, aiding informed analysis and decision-making.

Case Studies: Success Stories

There have been numerous success stories where identifying horizontal asymptotes contributed significantly to problem-solving or strategic advancements.

In the tech industry, a software company used horizontal asymptotes to model server performance and optimize resource allocation. By understanding the performance limits, they could prevent system overloads and enhance efficiency, leading to increased customer satisfaction.

In agriculture, a farming cooperative identified asymptotes when analyzing crop yield data. This allowed them to recognize the point of diminishing returns on fertilizer usage, optimizing input for maximum output, and reducing waste and expense.

In healthcare, a pharmaceutical company successfully enhanced its drug delivery models by leveraging asymptotes. Understanding the saturation levels in drug absorption led to more precise dosage designs, improving patient outcomes and reducing side effects.

These cases highlight how the practical application of horizontal asymptotes can drive efficiency and innovation across diverse sectors, fostering growth and improved outcomes through data-driven decision-making.

 

FAQs

What defines a horizontal asymptote?

A horizontal asymptote is a horizontal line that a graph approaches as x becomes very large (positive or negative). It shows the limiting value of a function’s output and is especially common in rational functions. This line represents a steady-state or saturation level that the function tends toward but doesn’t necessarily reach. It’s determined by analyzing the degrees and leading coefficients of the function’s numerator and denominator.

Can Excel find all types of asymptotes?

Excel is great for identifying horizontal asymptotes because you can easily simulate x-values, apply the function formula, and graph the output. It can help visualize vertical asymptotes as sharp spikes or gaps in the graph, though it won’t “label” them automatically. Oblique asymptotes are more complex and typically require manual calculations or polynomial division, though Excel can still graph the trend. So, while Excel doesn’t find them automatically, it’s excellent for exploring all three visually with the right prep.

How do I determine a horizontal asymptote in Excel?

Start by entering a wide range of x-values in one column, then apply your function using a formula in the next column. Based on the degrees of the numerator and denominator, calculate the horizontal asymptote value and enter it in a third column as a constant. Then create a scatter plot with smooth lines using all three columns. Excel will display both your function curve and the horizontal line, allowing you to see how the function approaches the asymptote.

What if I get errors while plotting asymptotes in Excel?

Errors like #DIV/0! or #VALUE! often occur if you forget to handle problematic x-values (like ones that make the denominator zero). Use formulas like =IFERROR((2*A2+3)/(A2+1), “”) to prevent chart-breaking errors. Also, double-check your formula syntax and make sure the ranges you’re using match across all columns. Keeping your spreadsheet clean and using conditional formatting can also help you spot data points that don’t align.

Why are horizontal asymptotes important in real-world data analysis?

They help model situations where growth or change plateaus, like population saturation, drug absorption limits, or market capacity. Recognizing horizontal asymptotes lets analysts understand the end behavior of systems, where things are heading in the long run. This is especially helpful in fields like pharmacokinetics, agriculture, economics, and engineering, where knowing the limits of a system guides smarter decisions. Excel’s ability to visualize this can make those patterns crystal clear.