How to Use Z Critical Value Calculator in Excel – Step by Step Guide

Navigating statistical analysis in Microsoft Excel requires a grasp of crucial concepts like the Z critical value. This value acts as a threshold for statistical significance, guiding your interpretation of data in the realm of standard normal distributions. Whether you’re delving into research, business analysis, or any field reliant on data-driven decisions, understanding how to use Z critical value calculator is indispensable.

Key Takeaways:

• Significance Threshold: The Z critical value sets the boundary for determining whether your results are statistically significant, aiding in decision-making processes.
• Standardization with Z Scores: Z scores offer a standardized way to compare data points across different scales, facilitating insightful analysis regardless of original units of measurement.
• Calculation in Excel: Excel’s built-in functions, like NORM.S.INV, streamline the process of computing Z critical values, providing a user-friendly platform for statistical analysis.
• Interpretation Insights: Interpreting Z critical values accurately is crucial; they indicate the significance of test results within the chosen confidence level, guiding your conclusions.

 

Introduction to Z Critical Value in Excel

Understanding the Z Critical Value

When you dive into the world of statistics, certain terms might seem confusing at first, but they’re crucial for precise data analysis. One such term is the Z critical value, which is what statisticians refer to when they’re dealing with standard normal distributions.

In simpler terms, it’s the threshold at which your results can be considered statistically significant. It helps you understand the ‘rareness’ of the result within the context of your data. If you’re someone who regularly uses Excel for statistical analysis, knowing how to find the Z critical value is an essential skill.

The Importance of Z Scores in Statistical Analysis

In statistical analysis, Z scores are incredibly important. They provide a clear, standardized method of comparison between different data points or sets. A Z score expresses the number of standard deviations a data point is from the mean. By converting raw scores into Z scores, you can understand a data point’s position relative to the overall dataset irrespective of the original units of measurement.

This becomes particularly useful in scenarios where you are comparing scores from different tests or measurements that may not use the same scale. With Z scores, these disparate sets of data can be normalized, enabling you to compare apples to oranges, so to speak. Additionally, Z scores are used in various statistical tests, such as the Z-test, to assess whether there is a significant difference between sample and population means.

Understanding Z scores equips you with the ability to identify outliers, understand the data distribution, and make informed decisions backed by statistics. Given the utility and versatility of Z scores, it’s evident why they are a cornerstone in the world of analytics.

 

Getting Started with Your Z Critical Value Calculator

Requirements for Using a Z Critical Value Calculator in Excel

Before you jump into calculating the Z critical value in Excel, there are a few prerequisites. First and foremost, you need a version of Excel that supports the statistical functions you’re planning to use. This usually means having the latest updates installed, which will ensure access to all the necessary features.

Second, a little background in statistics can go a long way. At a minimum, you should understand what a Z critical value is and why it’s significant for your analysis. You should also be familiar with terms like “confidence level,” “standard deviation,” and “mean” as they are key components of the calculation.

Lastly, ensure your data is ready for analysis. This means it should be inputted into Excel in a clean, organized manner – no missing values, and ideally, in a single column or row for easy reference. With these requirements in place, you’ll be set to compute the Z critical value smoothly and with confidence.

Step-by-Step Guide to Accessing the Functions

If you’ve got your data organized and a grasp on the basics of Z scores, accessing the functions in Excel needed for calculating the Z critical value is your next step. Here’s how to do just that:

STEP 1: Click on the cell where you would like to display your Z critical value.

STEP 2: Now, go to the ‘Formulas’ tab on Excel’s Ribbon, which is the toolbar you see at the top of Excel’s interface.

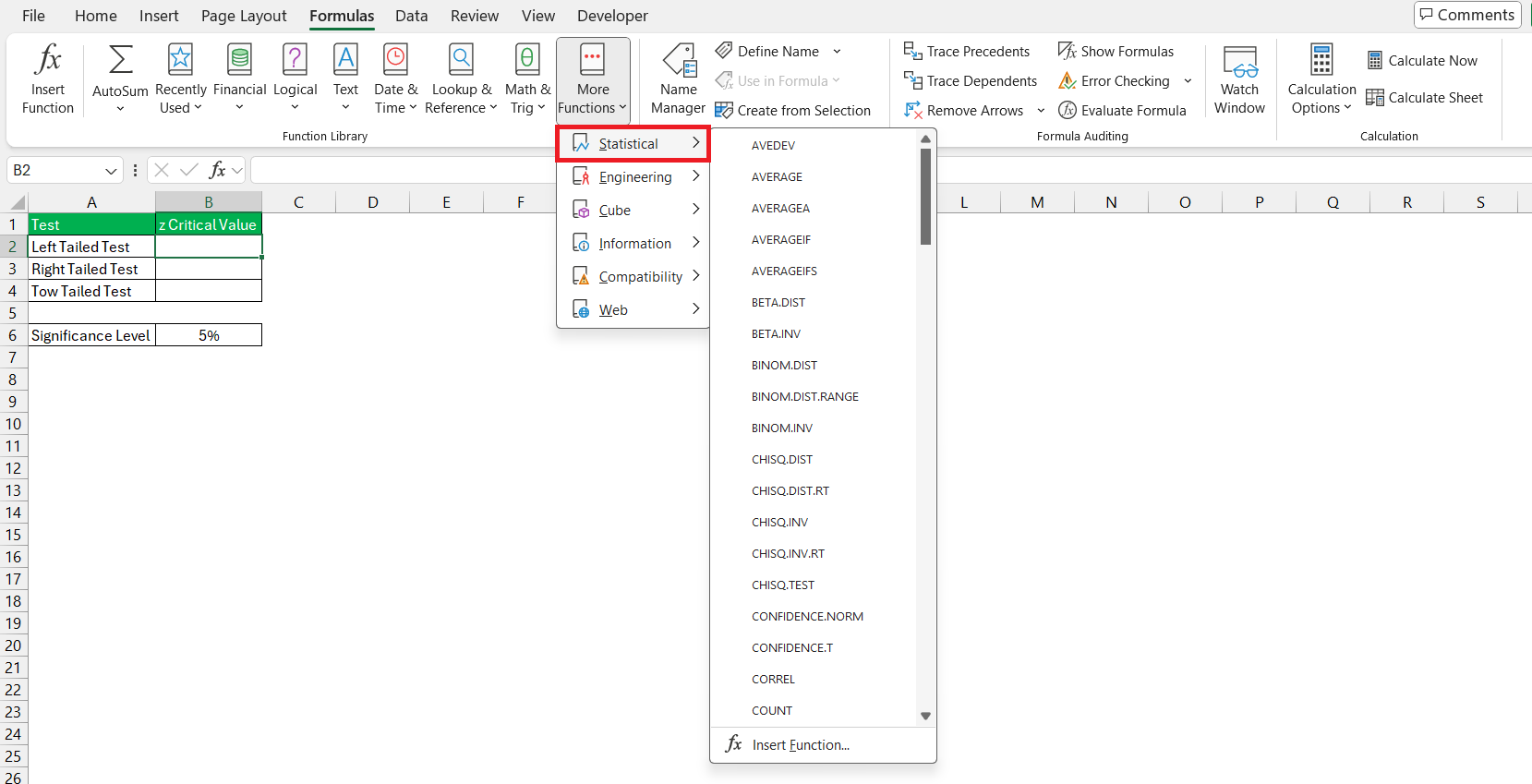
STEP 3: From there, look for the ‘Function Library’ group – this is where you’ll find built-in functions for various forms of analysis. Click on ‘More Functions,’ then hover over ‘Statistical’ to see a dropdown list of statistical functions.

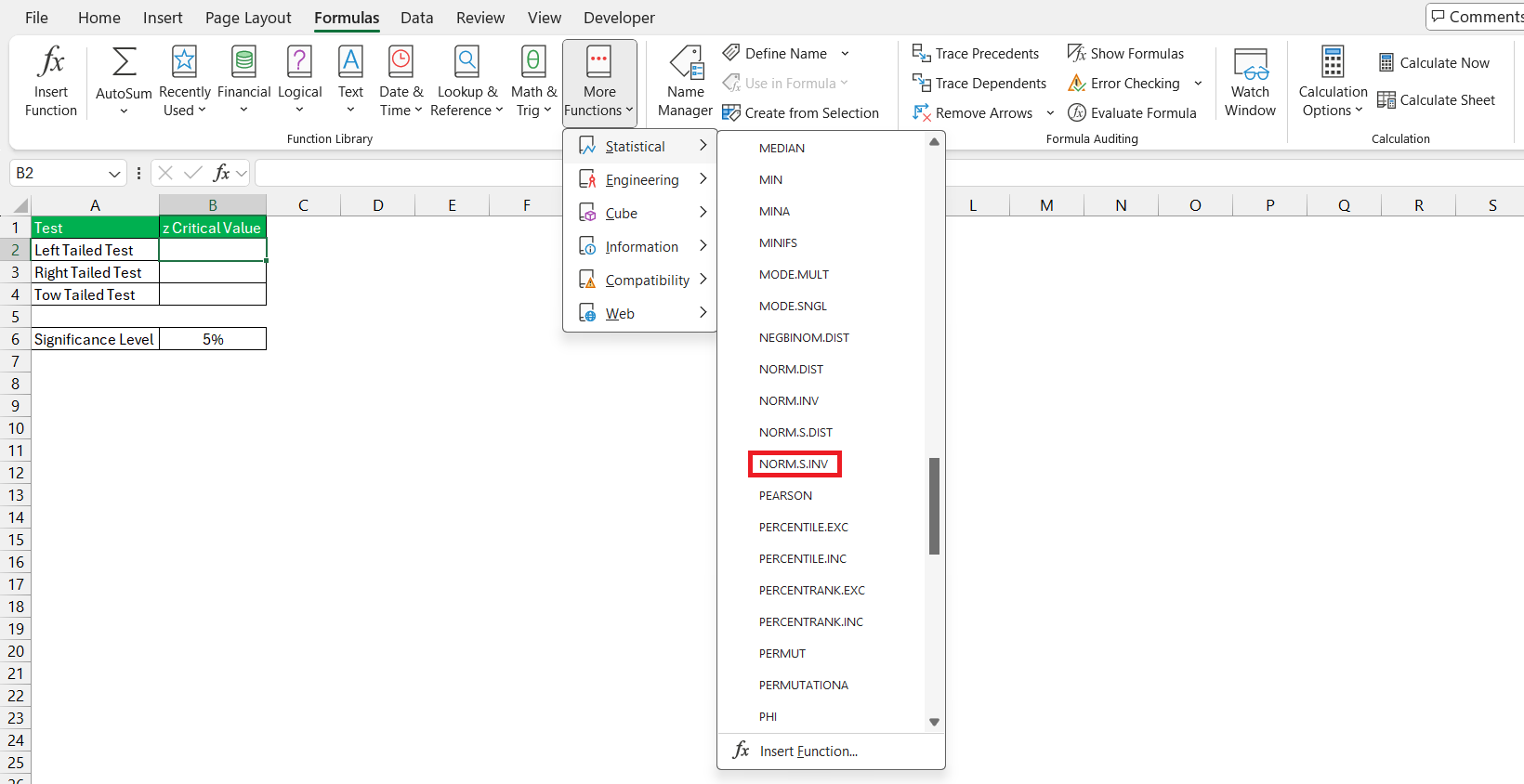
STEP 4: From the list, you will choose the function that corresponds to the Z critical value calculation; often, this is the ‘NORM.S.INV’ or ‘NORM.INV,’ depending on the specific analysis you’re conducting.

Remember that different versions of Excel may use slightly different paths or names for these functions. If you’re in doubt, the search feature in Excel’s ‘Help’ menu can be a quick way to find the proper function and how to use it for your version of Excel.

 

Calculating Z Critical Value: A Step-by-Step Process

Inputting Data: Where and How to Start

When you’re ready to calculate the Z critical value, your data must be accessible and neatly aligned. First things first – input your data. Usually, it’s best to place your data set in a single column for clarity and ease of use. Make sure there are no gaps or non-numeric entries that could skew your calculations.

After your data is in place, you need to define the significance level (alpha, α) for your analysis. This is the probability of rejecting the null hypothesis when it is actually true, and it’s commonly set at 0.05 for a 95% confidence level. However, the level you choose may vary based on the standards of your field or the specific requirements of your analysis.

With the significance level determined, you can now calculate the Z score that corresponds to that level. In Excel, you’ll likely use the NORM.S.INV function for this purpose. Here’s how you start:

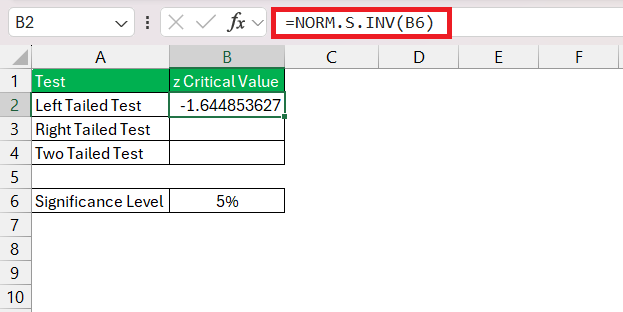
STEP 1: Click on an empty cell where you want the Z critical value to appear.

STEP 2: Enter “=NORM.S.INV(α)” into the cell, replacing α with your chosen significance level. Press ‘Enter,’ and Excel will calculate the Z critical value for you.

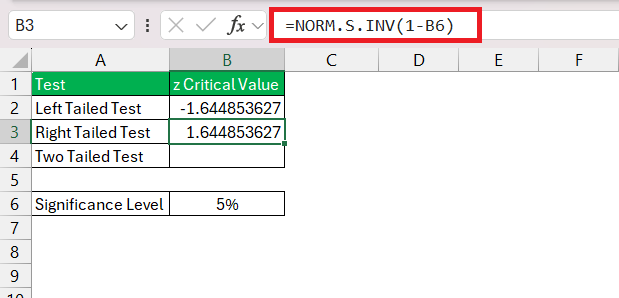
If you’re conducting a right-tailed test with a 95% confidence level, use this formula –

=NORM.S.INV(1-α)

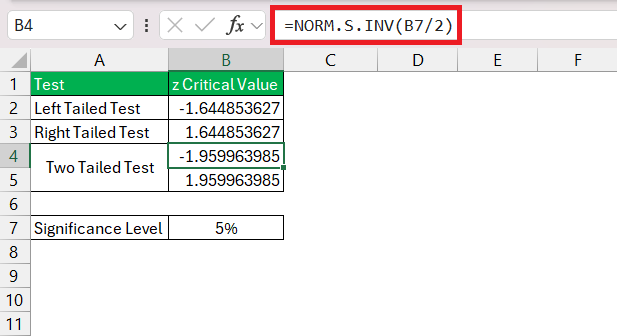
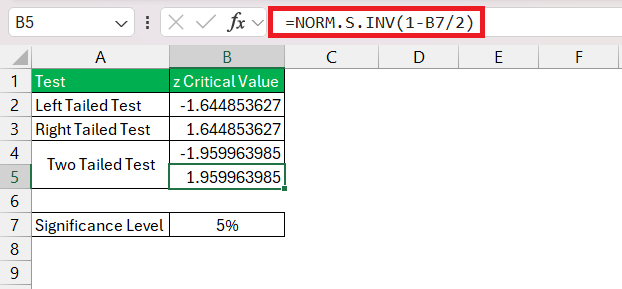
If you’re conducting a two-tailed test with a 95% confidence level, replace α with 0.025 (since each tail represents 2.5% of the total area under the curve).

Remember, precise data input is key. Any error in your data could lead to incorrect conclusions, so take your time and check your work. With these steps, you’ve made headway in your statistical analysis using Excel.

 

Making Sense of Your Results

Interpreting Z Critical Values in Excel

Once you’ve calculated the Z critical values in Excel, interpreting them correctly is essential to drawing accurate conclusions from your data. These values serve as the thresholds which determine the significance of your test results. Here’s what you need to keep in mind:

• If your Z test statistic exceeds the Z critical value in absolute terms, you would typically reject the null hypothesis. This would indicate that the test result is statistically significant, meaning it is unlikely to have occurred by random chance.
• In a one-tailed test, you compare your test statistic to one critical value on either the left or the right tail of the distribution, depending on your hypothesis.
• For a two-tailed test, you have two critical values to consider, corresponding to both tails. Your test statistic should fall outside of these two values to be considered significant.

Always remember that the Z critical value is connected to the confidence interval you chose. The more stringent the confidence level (like 99% instead of 95%), the farther the Z critical value will be from zero, making it a tougher threshold for your test statistic to exceed.

Interpreting these results in the context of your research enables you to make informed decisions or inferences, so take the time to understand what these numbers are telling you about the data you are analyzing.

Mistakes to Avoid When Using the Z Critical Value Calculator

When using the Z critical value calculator in Excel, accuracy is everything. To reduce the likelihood of errors, here are common mistakes you’ll definitely want to steer clear of:

1. Using The Wrong Function: Make sure to use the appropriate statistical function for calculating Z critical values (NORM.S.INV for standard normal distributions). Using the wrong function will lead to incorrect results.
2. Misplacing the Confidence Level: It’s common to mistakenly input the confidence level percentage rather than the alpha level (significance level) in the function. Remember, alpha is typically 1 minus the confidence level (e.g., for 95% confidence, alpha is 0.05).
3. Incorrect Tail Selection: Confusing one-tailed and two-tailed tests can happen. Ensure you use the correct formula for the type of test you’re conducting; they are not interchangeable.
4. Ignoring Data Range: Not properly extending your function to include the entire range of data can skew results. Confirm that you’ve selected the full dataset before calculating.
5. Data Entry Errors: Double-check all data entered in Excel. Simple mishaps like typos or misplaced decimals can significantly alter your Z critical value and subsequent interpretations.

By avoiding these pitfalls, you can trust your Z critical value calculations to be a solid foundation for your statistical analysis. Remember, these mistakes are not just about Excel proficiency; they also pertain to your grasp of statistical principles.

Practical Applications of Z Critical Values

Examples in Real-World Scenarios

Z critical values play an important role in many real-world scenarios, particularly in the fields of business, healthcare, and research:

• In market research, Z critical values help to determine whether changes in consumer satisfaction scores after a product update are statistically significant or if they could be attributed to chance.
• The healthcare industry relies on Z critical values to evaluate the effectiveness of new treatments. Researchers may utilize Z scores to decide if the recovery rates in the treatment group are significantly different from the recovery group under standard care.
• In finance, analysts might use Z critical values to assess whether the average returns on an investment over time are significantly different from the market average, helping to guide investment decisions.

By applying Z critical values to these real-world situations, professionals can make data-driven decisions with greater confidence, mitigating risk and identifying true signals amid the noise.

Enhancing Data Analysis Skills with Z Critical Values

Understanding and utilizing Z Critical Values enhance your data analysis skills by adding depth to your interpretative abilities. When you’re proficient in calculating and interpreting Z scores, you develop a stronger command of the statistical analysis, which allows you to:

• Make accurate predictions by setting appropriate confidence levels.
• Quantify the uncertainty in your predictions and estimates.
• Differentiate between random fluctuations in your data and meaningful patterns that warrant further investigation.
• Design and evaluate experiments or studies with increased rigor and precision.

By incorporating Z critical values into your analytical toolbox, you’re not just crunching numbers—you’re translating them into actionable insights that can inform strategies and decisions across various domains. Whether you’re in academia, industry, or any field that relies on data, mastering Z critical values is a step toward sharper, more reliable analysis.

 

Frequently Asked Questions

How do you calculate Zscore in Excel?

To calculate a Z score in Excel:

1. Input your data in one column.
2. Calculate the mean of your data using the formula: =AVERAGE(range).
3. Calculate the standard deviation with: =STDEV.S(range) for a sample or =STDEV.P(range) for a population.
4. Use the Z score formula: =(X-μ)/σ, replace ‘X’ with the cell of the data point, ‘μ’ with the mean, and ‘σ’ with the standard deviation.

Enter and execute this formula for each data point to get their Z scores.

What Does the Z Critical Value Represent?

The Z critical value represents a threshold in the standard normal distribution beyond which the observed data is considered statistically significant. Specifically, it determines the point at which you would reject the null hypothesis in a hypothesis test based on the chosen confidence level.

How Can I Find Z Critical Value Tables in Excel?

To find Z critical value tables in Excel, you cannot access them directly, but you can calculate Z critical values for specific confidence levels using Excel functions like NORM.S.INV().

Can I Use Z Critical Values for One-Tailed Tests?

Yes, Z critical values are used in one-tailed tests to determine the significance threshold. You use NORM.S.INV(1-α) for right-tailed tests and NORM.S.INV(α) for left-tailed tests, where ‘α’ is your significance level.

What Are Some Tips for Beginners Calculating Z Critical Values?

For beginners calculating Z critical values:

1. Understand the concept of Z scores and their role in hypothesis testing.
2. Learn the differences between one-tailed and two-tailed tests.
3. Familiarize yourself with Excel’s statistical functions.
4. Start with clean, well-organized data.
5. Practice with different data sets to reinforce your skills.